Answer:
The confidence interval is -5.3444 to 6.453 .
Explanation:
We are given that In a survey of 458 likely voters, 254 said that they would vote "yes" on the referendum.
So, n = 458
x = 254
We will use sample proportion over here

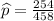
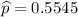
Confidence level = 95% = 0.95
Level of significance = 1-0.95 = 0.05
z value at 0.05 significance level = 1.96
Formula of confidence interval :
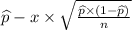 to
to
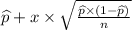
Confidence interval :
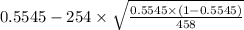 to
to
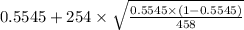
Confidence interval :
 to
to
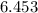
Hence The confidence interval is -5.3444 to 6.453 .