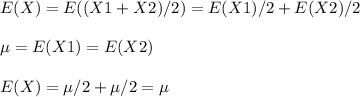Question

A particular brand of dishwasher soap is sold in three sizes: 25 oz, 45 oz, and 60 oz. Twenty percent of all purchasers select a 25-oz box, 50% select a 45-oz box, and the remaining 30% choose a 60-oz box. Let X1 and X2 denote the package sizes selected by two independently selected purchasers. (a) Determine the sampling distribution of X. x 25 35 45 42.5 52.5 60 p(x) Calculate E(X). E(X) = oz Compare E(X) to μ. E(X) > μ E(X) < μ E(X) = μ

Answer 1

(a) Sampling distribution

P(25) = 0,04

P(35) = 0.1 + 0.1 = 0,2

P(42,5) = 0.06 + 0.06 = 0,12

P(45) = 0,25

P(52,5) = 0.15 + 0.15 = 0,3

P(60) = 0,09

(b) E(X) = 45.5 oz

(c) E(X) = μ

Explanation:

The variable we want to compute is

`X=(X1+X2)/2`

For this we need to know all the possible combinations of X1 and X2 and the probability associated with them.

(a) Sampling distribution

Calculating all the 9 combinations (3 repeated, so we end up with 6 unique combinations):

P(25) = P(X1=25) * P(X2=25) = p25*p25 = 0.2 * 0.2 = 0,04

P(35) = p25*p45+p45*p25 = 0.2*0.5 + 0.5*0.2 = 0.1 + 0.1 = 0,2

P(42,5) = p25*p60 + p60*p25 = 0.2*0.3 + 0.3*0.2 = 0.06 + 0.06 = 0,12

P(45) = p45*p45 = 0.5 * 0.5 = 0,25

P(52,5) = p45*p60 + p60*p45 = 0.5*0.3 + 0.3*0.5 = 0.15 + 0.15 = 0,3

P(60) = p60*p60 = 0.3*0.3 = 0,09

(b) Using the sample distribution, E(X) can be expressed as:

`E(X)=\sum_(i=1)^(6)P_(i)*X_(i)\\E(X)=0.04*25+0.2*35+0.12*42.5+0.3*52.5+0.09*60 = 45.5`

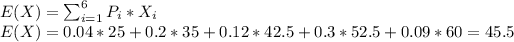
The value of E(X) is 45.5 oz.

(c) The value of μ can be calculated as

`\mu=\sum_(i=1)^(3)P_(i)*X_(i)\\\mu=0.2*25+0.5*45+0.3*60=45.5`

We can conclude that E(X)=μ

We could have arrived to this conclusion by applying

`E(X)=E((X1+X2)/2)=E(X1)/2+E(X2)/2\\\\\mu = E(X1)=E(X2)\\\\E(X)=\mu /2+ \mu /2 = \mu`