Answer:
Rate of heat loss=7992 kJ/h
Step-by-step explanation:
First, we can consider the room as a closed system, so we can use the first law of the thermodynamic:
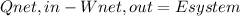
The incoming net heat is the incoming heat less the leaving heat, the leaving net work is the leaving work less the incoming work and the system energy is only the change of the intern energy because we have a stationary system, so:

From the problem we consider that there is no change of the temperature thus there is no change in the intern energy(U2=U1), moreover there is no incoming heat neither exit work, all the work is made to the system as a result the leaving heat is equal to the incoming work:
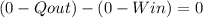
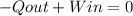
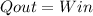
Substituting the known values we can get the rate of heat loss (exit heat):
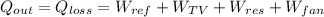
![Q_(loss)=250 [W]+120 [W]+1800 [W]+50 [W]](https://img.qammunity.org/2020/formulas/physics/college/7hdycwdsfwat7ca4lxxkifpyad8e2w6bgi.png)
![Q_(loss)=2220 [W]=2220 [(J)/(s) ]](https://img.qammunity.org/2020/formulas/physics/college/lrdqa184162w874jcl3lpi2nn36up9oimo.png)
Converting to Joules/hours:
![Q_(loss)=2220 [(J)/(s) ][(3600 s)/(1 h) ]](https://img.qammunity.org/2020/formulas/physics/college/gaj1hrwpnbmk61sd3hs8yynhte6180px1q.png)
![Q_(loss)=7992000 [(J)/(h) ]](https://img.qammunity.org/2020/formulas/physics/college/d3oagu3mya0twpzbh7g4ucsdvc9c0e2t2t.png)
Finally the rate of heat loss is:
![Q_(loss)=7992 [(kJ)/(h) ]](https://img.qammunity.org/2020/formulas/physics/college/nhu2bv3cp7c6rw5679divnoyn7ur2vhfed.png)