Question

3 points | Previous Answers LarCalcET6 8.8.012. Ask Your Teacher My Notes Question Part Points Submissions Used Explain why the integral is improper. 0 e7x dx −[infinity] At least one of the limits of integration is not finite. The integrand is not continuous on (-[infinity], 0]. Determine whether it diverges or converges. converges diverges Evaluate the integral if it converges. (If the quantity diverges, enter DIVERGES.)

Answer 1

The improper integral converges and
`\int_0^(-\infty) e^(7x)dx = -(1)/(7)`.

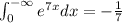Explanation:

First, I assume that the integral in question is

`\int_0^(-\infty) e^(7x)dx`.

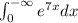Now, the integral is improper because, at least, one of the limits is
`\pm\infty`. We need to recall that an improper integral

`\int_0^(-\infty) f(x)dx`

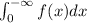
converges, by definition, if the following limit exist:

`\lim_(A\rightarrow -\infty) \int_0^A f(x)dx = \int_0^(-\infty) f(x)dx`.

In this particular case we need to study the limit

`\lim_(A\rightarrow -\infty) \int_0^A e^(7x)dx`.

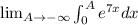In order to complete this task we calculate the integral
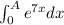`\int_0^A e^(7x)dx`. Then,

`\int_0^A e^(7x)dx = (e^(7x))/(7)\Big|_0^A = (e^(7A))/(7) - (1)/(7)`.

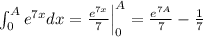Substituting the above expression into the limit we have

`\lim_(A\rightarrow -\infty) (e^(7A))/(7) - (1)/(7) = - (1)/(7)`

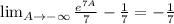
because

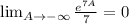`\lim_(A\rightarrow -\infty) (e^(7A))/(7)=0`.