Question

A small cruising ship that can hold up to 66 people provides three-day excursions to groups of 42 or more. If the group contains 42 people, each person pays $64. The cost per person for all members of the party is reduced by $1 for each person in excess of 42. Find the size of the group that maximizes income for the owners of the ship.

Answer 1

size of group is 53 people

Step-by-step explanation:

given data

person = 42

per person pay = $64

to find out

size of the group that maximizes income for the owners of the ship

solution

we will consider here number of additional person is = x

so

total passenger = x + 42

and price per person = 64 - x

so

total income is

R ( x) = ( x + 42 ) × ( 64 - x )

R ( x) = −x² + 22 x + 2688 .......................1

and maximize the total income will be when R (x) is a quadratic function

so

f (x) = ax² + bx + c is maximum

when a ≤ 0 and x =
`(-b)/(2a)`

so

income will maximum when x from equation 1

x =
`(-22)/(2(-1))`

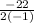
x = 11

so

size of group is 42 + 11 = 53