Question

A plane comes in for a landing at a velocity of 80 meters per second west. As it touches down, it decelerates at a constant rate of 3 meters per second per second. What is the minimum length of runway needed for this plane to come to a complete stop (on the runway!)?

OA) 240 m
OB) 682 m
OC) 859 m
OD) 1067 m​

Answer 1

Answer D : about 1067 meters

Step-by-step explanation:

There are two steps to this problem:

1) First find the time it takes the plane to stop using the equation for the acceleration:

`a=(Vf-Vi)/(t)`

Where Vf is the final velocity of the plane (in our case: zero )

Vi is the initial velocity of the plane (in our case: 80 m/s)

`a` is the acceleration (in our case -3 m/s^2 - notice negative value because the velocity is decreasing)

`a=(Vf-Vi)/(t)\\-3=(0-80)/(t)\\t=(-80)/(-3) = (80)/(3)`

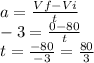
with units corresponding to seconds given the quantities involved in the calculation.

2) Second knowing the time it took the plane to stop, now use that time in the equation for the distance traveled under accelerated motion:

`Xf-Xi=Vi*t+(1)/(2) a t^(2) \\Xf-Xi= 80 ((80)/(3)) +(1)/(2) (-3) ((80)/(3)) ^(2)=1066.666666...`

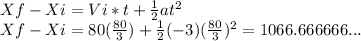
Where the answer results in units of meters given the quantities used in the calculation.

We round this to 1067 meters