Question

The number of people arriving for treatment at an emergency room can be modeled by aPoisson process with a rate parameter of 5/hr.(a) What is the probability thatexactly fourarrivals occur during a particular hour?(b) What is the probability thatat least threepeople arrive during a particular hour?(c) How many people do you expect to arrive during a45-minuteperiod?

Answer 1

(a) The probability of having exactly four arrivals during a particular hour is 0.1754.

(b) The probability that at least 3 people arriving during a particular hour is 0.7350.

(c) The expected arrivals in a 45 minute period (0.75 hours) is 3.75 arrivals.

Explanation:

(a) If the arrivals can be modeled by a Poisson process, with λ = 5/hr, the probability of having exactly four arrivals during a particular hour is:

`P(X=4)=(\lambda^(X)*e^(-\lambda)  )/(X!) =(5^(4)*e^(-5)  )/(4!)=(625*0.006737947)/(24) =(4.211)/(24)=0.1754`

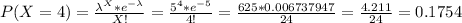
The probability of having exactly four arrivals during a particular hour is 0.1754.

(b) The probability that at least 3 people arriving during a particular hour can be written as

`P(X>3)=1-P(X\leq3)=1- (P(0)+P(1)+P(2)+P(3))`

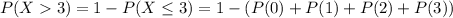
Using

`P(X)=(\lambda^(X)*e^(-\lambda)  )/(X!)`

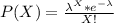
We get

`P(X>3)=1-P(X\leq3)=1- (P(0)+P(1)+P(2)+P(3))\\P(X>3)=1-(0.0067+ 0.0337+ 0.0842 + 0.1404 )\\P(X>3)=1-0.2650=0.7350\\`

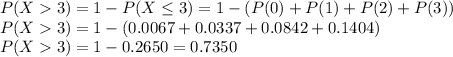
The probability that at least 3 people arriving during a particular hour is 0.7350.

(c) The expected arrivals in a 45 minute period (0.75 hours) is

`EV=\lambda*t=5*0.75=3.75`