Question

I need help with 11 and 12

Answer 1

Both are inverse pairs

Explanation:

Question 11

`g(x)= 4 + (8)/(5)x`

(a) Rename g(x) as y

`y = 4 + (8)/(5)x`

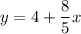
(b) Solve for x :

`(8)/(5)x = y - 4`

(c) Multiply each side by ⅝

`x = (5)/(8)(y - 4) = (5)/(8)y - (5)/(2)`

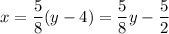
(d) Switch x and y

`y = (5)/(8)x - (5)/(2)`

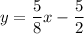
(e) Rename y as the inverse function

`g^(-1)(x) = (5)/(8)x - (5)/(2)`

(f) Compare with your function

`f(x) = (5)/(8)x - (5)/(2)\\\\f(x) = g^(-1)(x)`

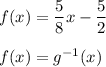
f(x) and g(x) are inverse functions.

The graphs of inverse functions are reflections of each other across the line y = x.

In the first diagram, the graph of ƒ(x) (blue) is the reflection of g(x) (red) about the line y = x (black)

Question 12

h(x)= x - 2

(a) Rename h(x) as y

y = x - 2

(b) Solve for x:

x = y + 2

(c) Switch x and y

y = x + 2

(e) Rename y as the inverse function

h⁻¹(x) = x + 2

(f) Compare with your function

f(x) = x + 2

f(x) = h⁻¹(x)

h(x) and ƒ(x) are inverse functions.

The graph of h(x) (blue) reflects ƒ(x) (red) across the line y = x (black).