Question

In a particular game, a fair die is tossed. If the number of spots showing is six you win $6, if the number of spots showing is five you win $3, and if the number of spots showing is four you win $1. If the number of spots showing is one, two, or three you win nothing. You are going to play the game twice. Each game is independent. The probability that you will win nothing on the two plays of the game is

Answer 1

Answer: Our required probability is 0.194.

Explanation:

Since we have given that

Amount win for showing 6 = $6

Amount win for showing 5 = $3

Amount win for showing 4 = $1

Amount win for showing 1, 2, 3 = $0

So,we need to find the probability that he will win nothing on the two plays of the game.

so, the outcomes would be

(1,1), (1,2), (1,3), (2,1), (3,1),(2,2), (3,3)

So, Number of outcomes = 7

total number of outcomes = 36

So, Probability of wining nothing =
`(7)/(36)=0.194`

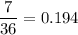
Hence, our required probability is 0.194.