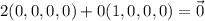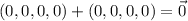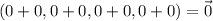Answer:
- B. The statement is false. The vector v1 could be the zero vector.
Step-by-step explanation:
Two vectors
 and
and
 are linearly independent if the equation
are linearly independent if the equation
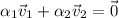
where
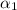 and
and
 are scalars, has only one solution:
are scalars, has only one solution:
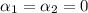 .
.
If there is more than one solution, we say that the vector are linearly dependent.
Why the answer is B. :
if
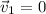 then,
then,
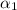 could have any value of the scalar group, as for any scalar
could have any value of the scalar group, as for any scalar

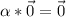
So, we get that there is more than one solution.
So, a particular counterexample is:

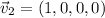
as
 is not an scalar multiple of
is not an scalar multiple of
 , and the equation
, and the equation
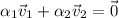
has as solution
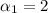
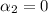
as we can see