Answer:
No. Both strategies has the same chance of success.
Step-by-step explanation:
The base strategy is let one dog choose the path. It has a chance of success of value
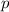 .
.
The strategy that the hunter uses is going wherever the two dogs go, if they choose the same, or pick a path 50-50, if they don't.
Probability of both dogs choosing the correct path =
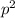
Probability of both dogs choosing the wrong path =
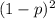
Probability of both dogs choosing different paths =
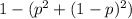
The probability of the hunter going the right path is
(Probability of both dogs choosing the correct path) + 0.5 * (Probability of both dogs choosing different paths)
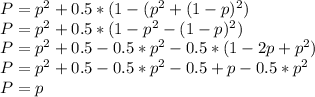
The probability of success of the hunter's strategy is the same as letting one dog decide one path.