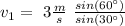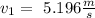Answer:
Step-by-step explanation:
For this problem, we just need to remember conservation of momentum, as there are no external forces in the horizontal direction:
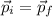
where the suffix i means initial, and the suffix f means final.
The initial momentum will be:
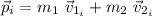
as the second puck is initially at rest:
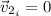
Using the unit vector
 pointing in the original line of motion:
pointing in the original line of motion:
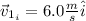
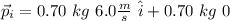
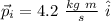
So:
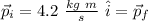
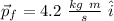
Knowing the magnitude and directions relative to the x axis, we can find Cartesian representation of the vectors using the formula
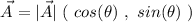
So, our velocity vectors will be:
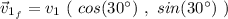
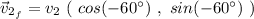
We got
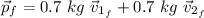
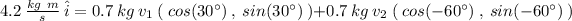
So, we got the equations:
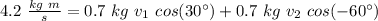
and
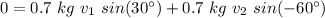 .
.
From the last one, we get:
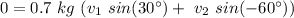
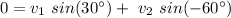
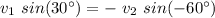
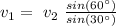
and, for the first one:
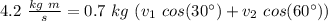
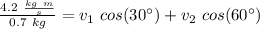
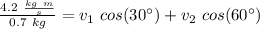
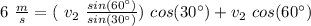
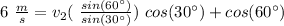
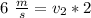
so:
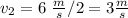
and