Answer:
The minimum sample size is 1867 observations.
Explanation:
We need to construct an 85% confidence interval that has an error less than 0.06. It means that the difference between the upper limit (UL) and the lower limit (LL) has to be 0.06.
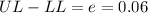
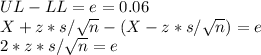
The only variable we can adjust is the number of observations (n)
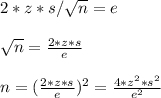
For a 85% confidence interval, the z-score is 1.440.
The estimated variance (s^2) is 0.81.
The error e is 0.06.
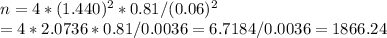
The sample has to be at least of 1867 observations.