Answer:
Critical value is 1.318 and the confidence interval is 29.357 to 33.042
Explanation:
n = 25
x = 31.2
s = 6.99
Degree of freedom = n-1= 25-1 =24
Confidence level = 0.8
So, α = 1- 0.8= 0.2
t critical =
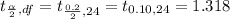
Formula of confidence interval :
 to
to

Confidence interval :
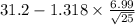 to
to
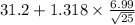
Confidence interval :
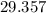 to
to
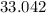
Hence critical value is 1.318 and the confidence interval is 29.357 to 33.042