Answer:
20 years.
Explanation:
We have been given a formula
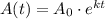 , which represents the value of an investment A (in dollars) after t years.
, which represents the value of an investment A (in dollars) after t years.
Substitute the given values:
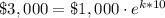
Let us solve for k.
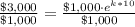
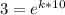
Take natural log of both sides:
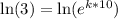
Using property
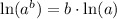 , we will get:
, we will get:
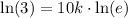
We know that
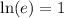 , so
, so
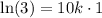
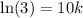
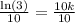
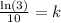
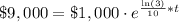
Dividing both sides by 1000, we will get:
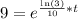
Take natural log of both sides:
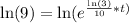
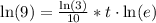
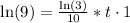
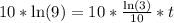
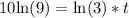
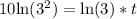
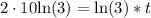
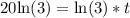
Divide both sides by
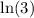 :
:
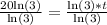
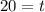
Therefore, it will take 20 years for the investment to be $9,000.