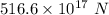Answer:
The weight of Earth's atmosphere exert is
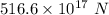
Step-by-step explanation:
Given that,
Average pressure
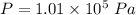
Radius of earth
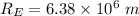
Pressure :
Pressure is equal to the force upon area.
We need to calculate the weight of earth's atmosphere
Using formula of pressure
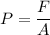
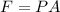
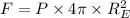
Where, P = pressure
A = area
Put the value into the formula
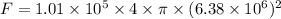
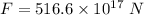
Hence, The weight of Earth's atmosphere exert is