Question

Determine whether each statement below is true or false. Justify each answer. a. A linear transformation is a special type of function. A. False. A linear transformation is not a function because it maps one vector x to more than one vector ​T(x​). B. True. A linear transformation is a function from set of real numbers R to set of real numbers R that assigns to each vector x in set of real numbers R a vector ​T(x​) in set of real numbers R. C. False. A linear transformation is not a function because it maps more than one vector x to the same vector ​T(x​). D. True. A linear transformation is a function from set of real numbers R Superscript n to set of real numbers R Superscript m that assigns to each vector x in set of real numbers R Superscript n a vector ​T(x​) in set of real numbers R Superscript m.

Answer 1

The correct answer is D.

Explanation:

In order to obtain the correct answer we need to recall the definition of function (or map) from one set to another. So, we say that a function (or map) is a way to associate a unique object to every element of a set. In a more mathematical formulation we say that
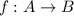`f:A\rightarrow B` is a function if, for every element
`a\in A` there exists a unique element
`f(a)=b\in B`.

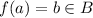We need to recall the definition of linear transformation too. So, we say that a map
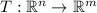`T: \mathbb{R}^n\rightarrow \mathbb{R}^m` is a linear transformation such that

• 
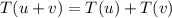  `T(u+v) = T(u) + T(v)`, for all
  `u,v\in\mathbb{R}^n`,

• 
  `T(\alpha u) = \alpha T(u), for every [tex]u\in\mathbb{R}^n` and every
  and
  `B=\mathbb{R}^m`,

• 
  `T=f`.

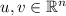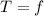Also, a linear transformation must satisfies the conditions stated in its definition.

Just notice that these are the explanation that comes with the option D.