Answer:
z-value = -3.4283
p-value = 0.0003
Explanation:
To find the standardized test statistic or z-value, we use the formula
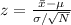
where
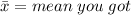
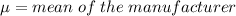
N = size of the sample.
So,
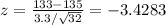
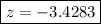
As your sampling suggests that the real mean could be less than the manufacturer's mean, then you are interested in the area under the normal curve to the left of -3.4283 and this would be your p-value.
We compute the area of the normal curve for values to the left of -3.4283 either with a table or with a computer and find that this area is equal to 0.0003.
So the p-value is
