Question

Assume that you wish to purchase a bond with a 30-year maturity, an annual coupon rate of 10 percent, a face value of $1,000, and semiannual interest payments. If you require a 9 percent nominal yield to maturity on this investment, what is the maximum price you should be willing to pay for the bond?

Answer 1

present value of the bond discounted at 9% $1,103.19

Step-by-step explanation:

We will calcualte the present value of the coupon payment and the maturity of the bonds a t the 9% market rate to know the present value of the bonds.

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

Cuopon payment: 1,000 x 10% /2 = $50 per payment

time 30 years x 2 payment per year = 60

rate 9% annual /2 = 4.5% semiannual = 0.045

`50 * (1-(1+0.045)^(-60) )/(0.045) = PV\\`

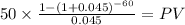
PV $1,031.9011

`(Maturity)/((1 + rate)^(time) ) = PV`

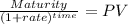
Maturity 1,000.00

time 60

rate 0.045

`(1000)/((1 + 0.045)^(60) ) = PV`

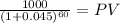
PV 71.2890

PV coupon payment $1,031.9011

PV maturity $71.2890

Total $1,103.1901