Answer: The given system of equations will have an infinite number of solutions.
Step-by-step explanation: We are given to find the solution to the following system of equations :

Dividing equation (i) by 3 and equation (ii) by -9, we get
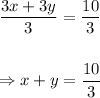
and
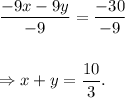
Since both the equations are same, so we have a linear equation in two variables x and y.
Therefore, the given system of equations will have an infinite number of solutions.