Answer:
The production level that maximizes Silky's profit is
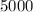 ties.
ties.
Step-by-step explanation:
Hi
First of all, as we have
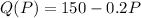 , we need to transcript it as price in function of the quantity so
, we need to transcript it as price in function of the quantity so
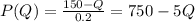
Then we need to find income function that is
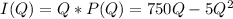 . After derivate it
. After derivate it
 .
.
The optimum level is when we have
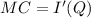 , therefore,
, therefore,
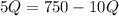 , as we clear it for
, as we clear it for
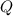 we find that
we find that
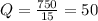 , finally as we have that
, finally as we have that
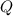 is measured in hundreds of ties, the production level that maximizes Silky's profit is
is measured in hundreds of ties, the production level that maximizes Silky's profit is
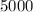 ties.
ties.