Question

the path of the longest shot put is modeled by h(x)=-1.017x^2+1.08x+5.8, x is the horizontal distance from start and h(x) is the height of the shot put above the ground. A) determine h(24), round to 2 decimal places. B) determine numerical value of the vertical intercept. C) determine numerical value of the vertex. D)how far from start did the shot put strike the ground

Answer 1

A) h(2.4) is 2.53

B) The numerical value of the vertical intercept is 5.8

C) The numerical value of the vertex is
`((60)/(113),(3439)/(565))`

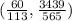
D) The shot put strike the ground at x = 2.98

Explanation:

* Lets explain how to solve the problem

- The path of the longest shot put is modeled by

h(x)= -1.017x² + 1.08x + 5.8, where x is the horizontal distance from

start and h(x) is the height of the shot put above the ground

A)

- We need to find h(2.4), that means substitute x in the equation by 2.4

∵ h(x)= -1.017x² + 1.08x + 5.8

∵ x = 2.4

∴ h(2.4)= -1.017(2.4)² + 1.08(2.4) + 5.8 = 2.53

∴ h(2.4) = 2.53

* h(2.4) is 2.53

B)

- We need to find the numerical value of the vertical intercept

- That means the y-intercept of the graph of the path ⇒ h(0)

- To find the vertical intercept put x = 0 in the equation

∴ h(0) = 0 + 0 + 5.8

* The numerical value of the vertical intercept is 5.8

C)

- We need to find the numerical value of the vertex

∵ h(x)= -1.017x² + 1.08x + 5.8 is a quadratic function

∴ The coordinates of its vertex are (v , w), where v
`(-b)/(2a)`

and w = h(v), a is the coefficient of x² and b is the coefficient of x

∵ a = -1.017 and b = 1.08

∴ v =
`(-1.08)/(2(-1.017))=(60)/(113)`

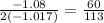
∵ w = f(v)

∴ w =
`-1.017((60)/(113))^(2)+1.08((60)/(113)) + 5.8=(3439)/(565)`

* The numerical value of the vertex is
`((60)/(113),(3439)/(565))`

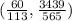
D)

- We need to find how far from start the shot put strike the ground

- That means h(x) = 0, because the height at the ground = 0

∴ -1.017x² + 1.08x + 5.8 = 0

- Use your calculator to find the value of x

∴ x = 2.977 and x = -1.915

- We will ignore the negative value of x because we need the final

put strike on the ground from the start

∴ x = 2.98

* The shot put strike the ground at x = 2.98