Question

Consider the initial value problemy' + 3 y = 36 t, y(0) = 6.Take the Laplace transform of both sides of the given differential equation to create the corresponding algebraic equation. Denote the Laplace transform of y(t) by Y(s). Do not move any terms from one side of the equation to the other (until you get to part (b) below).Solve your equation for Y(s).Y(s) = L{y(t)} =Take the inverse Laplace transform of both sides of the previous equation to solve for y(t).y(t) =

Answer 1

The solution of the differential equation is
`y(t) = -4 + 12t + 10e^(-3t)`.

Explanation:

The first step is to take Laplace transform in both sides of the differential equation. As usual, we denote the Laplace transform of
`y` as
`Y=L[y]`. Then,

`L[y'+3y](s) = L[36t](s)`

`L[y'](s)+3L[y](s) = 36L[t](s)`

`sY(s)-y(0)+3Y(s) = (36)/(s^2)`

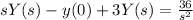
In the last step we use that
`L[y'](s) = sL[y](s)-y(0)` and
`L[t](s) = (1)/(s^2)`.

Notice that our differential equations becomes an algebraic equation for
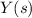`Y(s)`, which is more simple to solve.

In the expression we have obtained, we can write
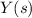`Y(s)` in terms of
`s`:

`(s+3)Y(s)-6=(36)/(s^2)` which is equivalent to

`Y(s) = (36)/(s^2(s+3)) +(6)/(s+3)`.

Now, we make a partial fraction decomposition for the term
`(36)/(s^2(s+3))`. Thus,

`(36)/(s^2(s+3)) = -(4)/(s) + (12)/(s^2) + (4)/(s+3)`.

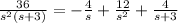Substituting the above value into the expression for
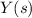`Y(s)` we get

) in both hands of the above expression. Recall that
`y(t) =  L^(-1)[Y](t)`. So,

`y(t) = L^(-1)\left[-(4)/(s) + (12)/(s^2) + (10)/(s+3)\right](t)`

`y(t) = -4L^(-1)\left[(1)/(s)\right](t) + 12L^(-1)\left[(1)/(s^2)\right](t) + 10L^(-1)\left[(1)/(s+3)\right](t)`

`y(t) = -4 + 12t + 10e^(-3t)`.

To obtain this we have used the following identities that can be found in any table of Laplace transforms

`L^(-1)\left[(1)/(s)\right](t) = 1`

`L^(-1)\left[(1)/(s^2)\right](t) = t`

`L^(-1)\left[(1)/(s+3)\right](t) = e^(-3t)`