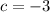Answer:
Equation of tangent of curve at x = 36:
1)
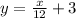
2
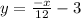
Explanation:
We are given the following information:
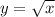
Value of curve when x = 36:

Thus,
 , when x = 6.
, when x = 6.
Slope of curve, m =
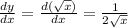
At x = 36,
slope of curve =

Equation of tangent of curve at x = 36:
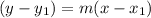

Thus, equation of tangents are:
1)
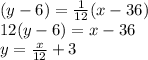
Comparing to
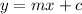 , we get
, we get
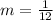 and
and

2)
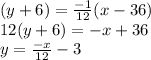
Comparing to
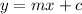 , we get
, we get
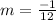 and
and