Question

Humerus bones from the same species of animal have approximately the same length-to-width ratios. It is known that Species A has a mean ratio of 8.5. Suppose that 41 fossil humerous bones were unearthed at a site where Species A is known to have flourished. (We assume that all bones are from the same species.) The length-to-width ratios of these bones has sample mean 9.26 and sample standard deviation 1.20. Can we conclude that these bones belong to Species A? Perform a level 0.05 z-test to check.

Answer 1

The unearthed Humerous bones don't belong to the species A.

Step-by-step explanation:

Hello!

You are studying the Humerus bones species A, who is known to have a mean ratio of 8,5. This value corresponds to the population mean of the length-to-with ratio of bones of species A, symbolized as μ.

The hypothesis you want to study is "The Humorous bones unearthed belong to the species A" if you assume this to be true, then the mean of the length-to-with ratio should be equal to the known population mean of the length-to-with ratio.

Symbolized:

H₀: μ = 8,5

H₁: μ ≠ 8,5

Significance level: α: 0,05

You are asked to use a Z-test, since you don't know the value of the population variance, but have the sample values, the sample size is big enough (more than n=30). Assuming that the sample values are independent, the statistic test of choice is the approximation:

`Z= \frac{x_bar-μ}{S\sqrt[]{n} }`≅N(0;1)

The critical region, in this case, it's a two-tailed test (remember the type is determined by the null hypothesis) so you'll have two critical values.

Left value [/tex]
`Z_(\alpha/2) = Z_(0,025) = -1,96`

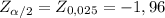
Right value
`Z_(1-\alpha/2) = Z_(0,975) = 1,96</p><p>So you'll reject the null hyphotesis if the calculated [tex]Z_(obs)` value is ≤-1,96 or ≥1,96 and you'll support it if -1,96<
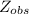`Z_(obs)`<1,96

Now we calculate the statistic by replacing the formula with the data:

x_bar = 9,26

S = 1,20

n = 41

`Z_(obs)= \frac{x_bar-μ}{S\sqrt[]{n} }`

`Z_(obs)= \frac{9,26-8,5}{1,20\sqrt[]{41} }`

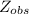`Z_(obs)`= 4,0553

Since the calculated value falls in the rejection region, this means, you have statistically significant results. In other words you can reject the null hipothesis (H₀: μ = 8,5) and asume that the unearthed Humerous bones don't belong to the species A.

I hope you have a SUPER day!