Question

While her kid brother is on a wooden horse at the edge of a merry-go-round, Sheila rides her bicycle parallel to its edge. The wooden horses have a tangential speed of 6 m/s. Sheila rides at 4 m/s. The radius of the merry-go-round is 8 m.. At what time intervals does Sheila encounter her brother, if she rides in the direction of rotation of the merry-go-round?

Answer 1

25.12 seconds

Explanation:

As we have been given ion the question,

Tangential speed of her brother at the Wooden Horse = 6 m/s

Tangential speed of Sheila = 4 m/s

Radius of merry go round, r = 8 m

Now,

We know that,

v = r.ω

So,

Angular velocity of brother is given by,

`v=r.\omega\\\omega = (v)/(r)=(6)/(8)\\\omega =0.75\,rad/sec.`

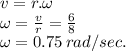
And,

Angular velocity of Sheila is given by,

`v=r.\omega\\\omega = (v)/(r)=(4)/(8)\\\omega =0.5\,rad/sec.`

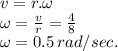
Relative Angular Velocity = 0.75 - 0.5 = 0.25 rad/s.

Therefore, the time taken by Sheila to encounter her brother again is given by,

`Time=(Total\,Distance)/(Relative\,Speed)\\Time=(2\pi)/(0.75-0.5)\\Time,t=(2\pi)/(0.25)\\t=8\pi\\Time,t=25.12\,s`

Therefore, Time Taken to encounter again is 25.12 seconds.