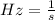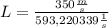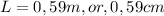Answer:
The answer is about 0,59 m or 59 cm the longest wavelength for a listener when the sirens is closest.
Step-by-step explanation:
Using the equation of the effect Doopler:
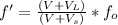
Replacing:
W angular velocity = 0,8
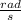
V = 350
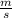
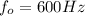
VL = 0
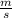
/(s)](https://img.qammunity.org/2020/formulas/physics/college/n745tbdndomv457cg7eoawk2wn7wo7k19e.png) * 5 m
* 5 m
Vs = 4
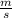
Replacing:
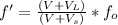
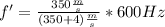
Note: Notice, the division have the same units so, it can be simplify
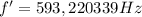
Now using the frequency f' as the frequency of the listener to know L wavelength as the relation between f' and V
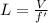
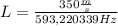
Note: Remember Hz units are relations inverse of time so: