Question

Consider a binomial distribution of 200 trials with expected value 80 and standard deviation of about 6.9. Use the criterion that it is unusual to have data values more than 2.5 standard deviations above the mean or 2.5 standard deviations below the mean to answer the following questions.

(a) Would it be unusual to have more than 120 successes out of 200 trials? Explain.

(A) Yes. 120 is more than 2.5 standard deviations above the expected value.
(B) Yes. 120 is more than 2.5 standard deviations below the expected value.
(C) No. 120 is less than 2.5 standard deviations above the expected value.
(D) No. 120 is less than 2.5 standard deviations below the expected value.

Answer 1

The correct answer is option 'a' : 120 is more than 2.5 standard deviations above the expected value.

Explanation:

For an exponential distribution we have

The expected value μ = 80

No of trails n = 200

Thus we have

`p=(80)/(200)=0.4`

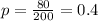
The deviation is related to expected value and probability as

`\sigma =√(np(1-p))\\\\\therefore \sigma =√(200\cdot 0.4\cdot (1-0.4))=6.9`

Thus the values between the given deviation is

`x_(1)=80-2.5* 6.9=62.75\\\\x_(2)=80+6.9* 2.5=97.25`

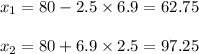
Now since 120 successes are out of the range of [62.75,97.25] thus 120 is more than the expected value.