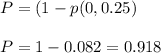Question

Airline passengers arrive randomly and independently at the passenger-screening facility

at a major international airport. The mean arrival rate is 10 passengers per minute.
a. Compute the probability of no arrivals in a one-minute period.
b. Compute the probability that three or fewer passengers arrive in a one-minute period.
c. Compute the probability of no arrivals in a 15-second period.
d. Compute the probability of at least one arrival in a 15-second period.

Answer 1

Answer with Step-by-step explanation:

Since the random arrival process follows a poission's distribution

The probability of 'n' arrivals in time 't' is given by

`P(n,t)=((\lambda t)^ne^(-\lambda t))/(n!)`

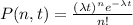
where

`\lambda` is the average rate of arrival given as 10 passengers per minute

Part a)

`P(0,1)=((10)^0\cdot e^(-10))/(0!)=0.0000454`

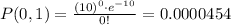
Part b)

The probability that 3 or lesser passengers arrive in 1 minute is the sum of the probabilities of arrival of no passenger , 1 passenger , 2 passengers or 3 passengers respectively

`P(E)=((10)^0e^(-10))/(0!)+((10)^1e^(-10))/(1!) +((10)^2e^(-10))/(2!)+((10)^3e^(-10))/(3!)=0.01033`

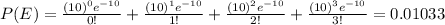
Part c)

Since 15 seconds correspond to 0.25 minutes we have

`P(0,0.25)=((10* 0.25)^0\cdot e^(-10* 0.25))/(0!)=0.082`

Part d)

Probability of at least one arrival in 15 seconds is

`P=(1-p(0,0.25)\\\\P=1-0.082=0.918`