Question

Methane, CH4, reacts with I2 according to the reaction CH4(g)+I2(g)⇌CH3I(g)+HI(g)

At 630 K, Kp for this reaction is 2.26×10−4. A reaction was set up at 630 K with initial partial pressures of methane of 105.1 torr and of 7.96 torr for I2.
Calculate the pressure, in torr, of CH4.
Express your answer to four significant figures and include the appropriate units.
Calculate the pressure, in torr, of I2.
Express your answer to three significant figures and include the appropriate units.
Calculate the pressure, in torr, of CH3I.
Express your answer to three significant figures and include the appropriate units.
Calculate the pressure, in torr, of HI.
Express your answer to three significant figures and include the appropriate units.

Answer 1

0.422 torr

Step-by-step explanation:

First you want to set up a table with three rows. Initial partial pressure, change in partial pressure, and equilibrium partial pressure. Make four columns, CH4, I2, CH3I,and HI. You are given the initial pressures of 105.1 torr and 7.96 torr for methane and I2. Put these in the respective row and column. In terms of change, CH4 would be -x due to the coefficient of 1, I2 would be -x as well. CH3I and HI would both be +x in terms of change. Initial+ change = equilibrium. So the equilibrium of methane is 105.1 torr-x and I2 is 7.96-x. Since the initial pressures of CH3I and HI are not given, they can be assumed to be zero, and therefore have equilibrium of +x. Kp = [HI][CH3I]/[CH4][I2]. Therefore, Kp= x^2/ (105.1-x)(7.96-x). Plug in the value of Kp and solve for x. The value of x should be roughly .42217 M. Now, since CH4 is 105.1-x, then 105.1-.42217= 104.7 torr. Following suit, I2= 7.96-.x and therefore 7.96-.42217= 7.54 torr. Since the equilibrium of CH3I and HI is just +x, the value of the equilibrium will just be .42217.

So:

CH4= 104.7 torr

I2= 7.54 torr

CH3I and HI= .422 torr

Answer 2

pCH₄ = 105.1 - 0.42 = 104.68 torr

pI₂ = 7.96 -0.42 = 7.54 torr

pCH₃I = 0.42 torr

pHI = 0.42 torr

Step-by-step explanation:

Kp is the equilibrium constant for the partial pressure of the gases in the reaction, and it is calculated for a general equation:

aA(g) + bB(g) ⇄ cC(g) + dD(g)

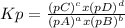`Kp = ((pC)^cx(pD)^d)/((pA)^ax(pB)^b)`, where p is the partial pressure in the equilibrium. By the reaction given:

CH₄(g) + I₂(g) ⇄ CH₃I(g) + HI(g)

105.1 torr 7.96 torr 0 0 initial partial pressure

-x -x +x +x react

105.1-x 7.96-x x x equilibrium

Then:

`Kp = (pCH3IxpHI)/(pCH4xpI2) = (x^2)/((105.1-x)(7.96-x))`

`2.26x10^(-4) = (x^2)/(836.596 - 113.06x -x^2)`

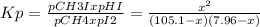
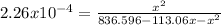
x² = 0.1891 - 0.0255x -2.26x10⁻⁴x²

0.9997x² + 0.0255x - 0.1891 = 0

Using Bhaskara's rule:

Δ = (0.0255)² - 4x(0.9997)x(-0.1891)

Δ = 0.7568

`x = (-b+/-√(0.7568) )/(2a) = (-0.0255 +/-0.8699)/(1.9994)`

Using only the positive term, x = 0.42 torr.

So,

pCH₄ = 105.1 - 0.42 = 104.68 torr

pI₂ = 7.96 -0.42 = 7.54 torr

pCH₃I = 0.42 torr

pHI = 0.42 torr