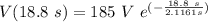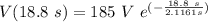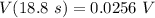Answer:
- a.

- b.
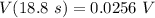
Step-by-step explanation:
a.
The equation for the voltage V of discharging capacitor in an RC circuit at time t is:
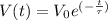
where
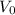 is the initial voltage, and
is the initial voltage, and
 is the time constant.
is the time constant.
For our problem, we know
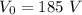
and
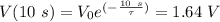
So

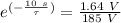
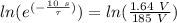


This gives us

and this is the time constant.
b.
At t = 18.8 s we got: