Answer:
Option B.
Explanation:
Consider the below figure attached with this question.
Formula for standard deviation of a sample:
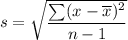
where, n is sample size and
 is sample mean.
is sample mean.
The sample data set is 12, 14, 9, and 21.
The mean is 14.
So, the sample standard deviation is
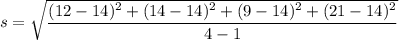
According to Yuri,
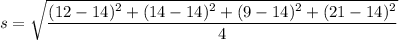
Yuri divides the sum of square of difference between each data point and the mean by n instead of n -1.
Therefore, the correct option is B.