Question

M5_A3. The expected project completion time for the construction of a pressure vessel is 18 monthsand the project variance is 7. (Note: when using the Z tables – round your Z values to two decimal placesbefore getting the probabilities from the tables. DO NOT round standard deviations prior to calculating Zvalues)NOTE: Enter probabilities as decimals (i.e 92.31% should be entered as 0.9231)a) What is the probability that the project will require at least 19 months? (Enter 4 decimal placesfrom distribution tables)b) What is the probability that the project will be completed within 24 months? (Enter 4 decimalplaces from distribution tables)c) What is the probability that the project will require at least 21 months? (Enter 4 decimal placesfrom distribution tables)d) What is the probability that the project will be completed within 15 months? (Enter 4 decimalplaces from distribution tables)e) What is the probability that the project will take between 16 and 24 months to complete? (Enter4 decimal places from distribution tablesShow Work

Answer 1

a) 0.3520

b) 0.9884

c) 0.1292

d) 0.1292

e) 0.7648

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by

`Z = (X - \mu)/(\sigma)`

After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X.

In this problem, we have that:

The expected project completion time for the construction of a pressure vessel is 18 months. So
`\mu = 18`.

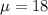And the project variance is 7. The standard deviation is the square root of the variance, so
`\sigma = √(7)`.

a) What is the probability that the project will require at least 19 months?

The pvalue of the zscore of
`X = 19` is the probability that the project will require less than 19 months. So the probability that the project will require at least 19 months is the subtraction of 1 by this pvalue.

`Z = (X - \mu)/(\sigma)`

`Z = (19 - 18)/(√(7))`

`Z = 0.38`

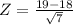
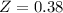
The pvalue of Z = 0.38 is 0.6480.

So the probability that the project will require at least 19 months is 1 - 0.6480 = 0.3520.

b) What is the probability that the project will be completed within 24 months?

This is the pvalue of the zscore of X = 24.

`Z = (X - \mu)/(\sigma)`

`Z = (24 - 18)/(√(7))`

`Z = 2.27`

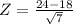
The pvalue of Z = 2.27 is .9884. This means that the probability that the project will be completed within 24 months is .9884.

c) What is the probability that the project will require at least 21 months?

Same logic as a). We find the pvalue of the zscore of X = 21, then we subtract 1 by this value.

`Z = (X - \mu)/(\sigma)`

`Z = (21 - 18)/(√(7))`

`Z = 1.13`

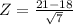
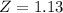
The pvalue of Z = 1.13 is 0.8708.

So the probability that the project will require at least 21 months is 1 - 0.8708 = 0.1292.

d) What is the probability that the project will be completed within 15 months?

Same logic as b). This is the pvalue of the zscore of X = 15.

`Z = (X - \mu)/(\sigma)`

`Z = (15 - 18)/(√(7))`

`Z = -1.13`

The pvalue of Z = -1.13 is .1292. This means that the probability that the project will be completed within 15 months is .1292.

e) What is the probability that the project will take between 16 and 24 months to complete?

This is the pvalue of Z = 24 subtract by the pvalue of Z = 16.

In b), we found that the pvalue of Z = 24 is .9884

Now we find the pvalue of Z = 16

`Z = (X - \mu)/(\sigma)`

`Z = (16 - 18)/(√(7))`

`Z = -0.76`

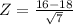
The pvalue of Z = -0.76 is 0.2236

So the probability that the project will take between 16 and 24 months to complete is 0.9884 - 0.2236 = 0.7648