Question

The mean number of close friends for the population of people living in the U.S. is 5.7. The standard deviation of scores in this population is 1.3. An investigator predicts that the mean number of close friends for introverts will be significantly different from the mean of the population. The mean number of close friends for a sample of 26 introverts is 6.5. Do these data support the investigator's prediction? Use an alpha level of .05.

Answer 1

The investigators prediction was right that the mean number of close friends of introvert are different from the mean of the population

Explanation:

We are given the following in the question:

Population mean, μ = 5.7

Sample mean,
`\bar{x}` = 6.5

Sample size, n = 26

Alpha, α = 0.05

Population standard deviation, σ = 1.3

First, we design the null and the alternate hypothesis

`H_(0): \mu = 5.7\text{(Mean number of close friends of introverts is same as the population)}\\H_A: \mu \\eq 5.7\text{(Mean number of close friends of introvert is not same as the population)}`

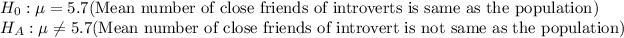
We use Two-tailed z test to perform this hypothesis.

Formula:

`z_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) }`

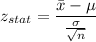
Putting all the values, we have

`z_(stat) = \displaystyle(6.5 - 5.7)/((1.3)/(√(26)) ) = 3.138`

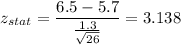
Now,
`z_(critical) \text{ at 0.05 level of significance } = 1.96`

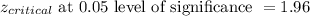
Since,

`z_(stat) > z_(critical)`

We reject the null hypothesis and accept the alternate hypothesis. Thus, the investigators prediction was right that the mean number of close friends of introvert are different from the mean of the population.