Answer:
Explanation:
According to the information given in the statement, there are the following mathematical expressions:

Where
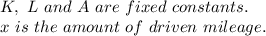
Considering
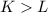
Then
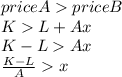
The last equation means that to maintain the [text]priceB[\text] lower than [text]priceA[\text], the amount of driven mileage must be less than
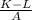 . If [tex]x[\tex] becomes greater than the fraction, then the [text]priceA[\text] will be lower than [text]priceB[\text].
. If [tex]x[\tex] becomes greater than the fraction, then the [text]priceA[\text] will be lower than [text]priceB[\text].
[tex]\frac{K - L}{A} < x \\ K - L < Ax \\ K < L + Ax[\tex]