Question

Seventy-three percent of products come off the line ready to ship to distributors. Your quality control department selects 12 products randomly from the line each hour. Looking at the binomial distribution, if fewer than how many are within specifications would require that the production line be shut down (unusual) and repaired?

Answer 1

If in the 12-unit sample less than 4 units are ready for shipping is abnormal for that process and the line should be shut down and repaired.

Step-by-step explanation:

According to the statements, 73% come off the line rady to ship. That mean a p=0.73 proportion of success.

To be abnormal, we can say that this proportion has to be 3σ below this mean value (p=0.73).

The standard deviation σ can be calculated as

`\sigma=√(n*p(1-p))`

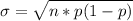
In this case, our sampling is n = 12 units, so we have

`\sigma=√(n*p(1-p))\\\\\sigma=√(12*0.73(1-0.73))\\\\\sigma=√(2.3652)\\\\\sigma=1.538`

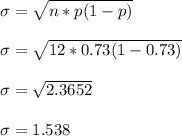
Then we can calculate the lower limit we can accept as normal in this 12-unit sample:

`LL=\bar{x}-3*\sigma=0.73*12-3*1.538\\\\LL=8.760-4.614=4.146`

We can conclude that if in the 12-unit sample less than 4 units are ready for shipping is abnormal for that process and the line should be shut down and repaired.