Question

Consider four different stocks, all of which have a required return of 15 percent and a most recent dividend of $4.20 per share. Stocks W, X, and Y are expected to maintain constant growth rates in dividends for the foreseeable future of 10 percent, 0 percent, and –5 percent per year, respectively. Stock Z is a growth stock that will increase its dividend by 20 percent for the next two years and then maintain a constant 10 percent growth rate thereafter. What is the dividend yield for each of these four stocks

Answer 1

Dividend yield for W = 5%

Dividend yield for X = 15%

Dividend yield for Y = 20%

Dividend yield for Z = 4.6%

Step-by-step explanation:

For a constant growth stock
`Price =(D1)/(r-g)`

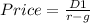
If r is made subject of formula; r=
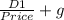`(D1)/(Price)+g` = div yield + growth rate

For Stock W, given r = 15% and g= 10%; dividend yield = 15%-10%=5%

For Stock X, given r = 15% and g= 0%; dividend yield = 15%-0%=15%

For Stock Y, given r = 15% and g= -5%; dividend yield = 15%-(-5)%=20%

For Stock Z, the price of the stock today is calculated as follows:

Price of the stock today =
`(D1)/((1+ke)^1)+(D2)/((1+ke)^2)+(P2)/((1+ke)^2)`.

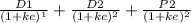where P2=
`(D3)/(ke-g)`

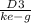
Price of the stock today =
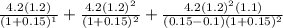`(4.2(1.2))/((1+0.15)^1)+(4.2(1.2)^2)/((1+0.15)^2)+(4.2(1.2)^2(1.1))/((0.15-0.1)(1+0.15)^2)`=109.57

Therefore dividend yield =
`\frac[D1}{Price}` =
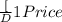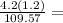`(4.2(1.2))/(109.57)=`4.6%