Answer:
The volume of the solid = π²
Explanation:
As per the given data of the questions,
The diameter of each disk is
D = 2 sin(x) - 2 cos(x)
So its radius is
R = sin(x) - cos(x).
The area of each disk is
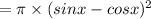
![= \pi * [sin^(2)(x) - 2 sin(x) cos(x) + cos^(2)(x)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/c9nfl7027kftfibk8t7gf063gi3jwjlweh.png)
![= \pi[1-2sin(x)cos(x)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/1gdp1ltuf6o5xpfy3ynzwc7lhbn5s0mwlp.png)
![= \pi[1-sin(2x)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/yw6dtpka578x0q47odzdjvz79jmhsnv2xh.png)
Now,
Integrate from
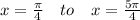 , we get volume:
, we get volume:
![V=\int_{(\pi)/(4)}^{(5\pi)/(4)} \pi[1-sin(2x)]dx](https://img.qammunity.org/2020/formulas/mathematics/high-school/zia95v2p8cqbp88v9srjv9sc8x0zp56noh.png)
After integrate without limit we get
![V=\pi[x+(cos2x)/(2)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/wz9zog5155zsmcgsfnn2al932ljrnyl8rh.png)
Now after putting the limit, we get
V = π²
Hence, the required volume of the solid = π²