Step-by-step explanation:
Let us take the equilibrium temperature is T.
Now, the heat absorbed by the ice is equal to the heat lost to the water.
Therefore, the formula will be as follows.

Therefore, putting the given values into the above formula as follows.

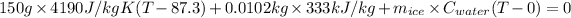
628500T - 54868050 + 3.3966 + 42.738T = 0
T =
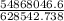
=
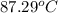
or, = (87.29 + 273.15)K
= 360.44 K
Since, formula for entropy change of ice is as follows.
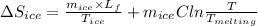
=
![\frac{0.0102 [(333000)/(273.15) + 4190 * ln ((360.44)/(273.15))]]()
=
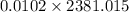
= 24.286 J/K
Entropy change for water (
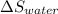 ) =
) =
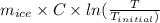
=
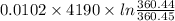
=
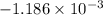 J/K
J/K
Therefore, calculate the net change in entropy as follows.
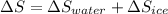
=
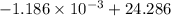 J/K
J/K
= 24.28481 J/K
Thus, we can conclude that the net entropy change of the system from then until the system reaches the final (equilibrium) temperature is 24.28481 J/K.