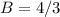Answer:
The numbers are
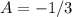 and
and
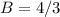 , and the sum of
, and the sum of
 is 1.
is 1.
Explanation:
We already know that the partial fraction decomposition of the rational fraction
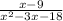 has a particular form, that is
has a particular form, that is
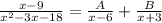 .
.
So, the method to find the coefficients
 and
and
 is:
is:
First: We calculate the sum
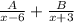 .
.
So,
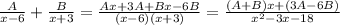 .
.
Notice that
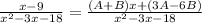 ,
,
which means that necessarily
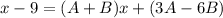 .
.
Second: We equalize the coefficients of the same powers of
 .
.
The last equality we have obtained means that
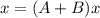 and
and
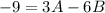 .
.
From the above statement we deduce that
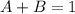 .
.
Third: We obtain a linear system of equations, with the unknowns
 and
and
 .
.
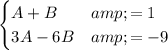
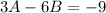
The solutions to these system of equations are
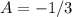 and
and