Answer:
a) 19.96 [m/s]
b) 3.26 [s]
c) 13.02 [m]
Step-by-step explanation:
Use the equations for linear motion:
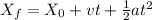
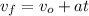
Since we have motion in the horizontal and vertical directions, we need to break down the problem by solving each direction separately. The first thing they ask for is the speed of the ball when it hits the ground. This will require finding the magnitude of the velocity vector when the ball hits the ground. As we know, it will have two velocity components, one in "x" and one in "y".
X component:
We have no accelerations acting on x, therefore:
Y component:
We can´t solve this equation yet as we don´t know how long it takes the ball to hit the ground. We´ll use this equation later.
The second question is how long does the ball remain in the air. We need to find a position of the ball where we can satisfy the equation and solve it. If you think about it, right at mid-flight, the ball is at maximum height and the ball has no velocity component in y (because it just transitioned from going up to going down), we can rewrite the equation as follows:
Solve for time in the equation which is half of the total time the ball is in the air:
And finally, multiply times 2 to get the total time the ball is in the air:
We can now go back to the first question and input the total time in the equation to find out the the velocity at which the ball hits the ground in the vertical direction:
We have the components, and all we need to do is find the root square of their squares (pythagoras theorem) to find the magnitude which equals the speed:
The third question is about the maximum height attained by the ball. We know the time when the ball was at its maximum height to be 1.63 [s], and we can use equation 1 to figure out the maximum height as follows:
If we make the ground our reference then hmax is positive going upwards:
Solving for hmax