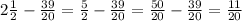Question

Matt wants to shave 2 1/2 minutes off his 5K race time. After a month of hard training, he managed to lower his overall time from 21 1/5 minutes to 19 1/4 minutes. By how many more minutes does Matt need to lower his race time?

PS: Solve the problem using the RDW strategy. Show all of your work.

Answer 1

The answer is 11/20 minutes.

Explanation:

First, you have this information:

• Matt wants to shave 2 1/2 mins.
• Before training: overall time 21 1/5 mins.
• After training: overall time 19 1/4 mins.

Now, you have to do the difference between 21 1/5 and 19 1/4, to know how much time Matt shaved.

You have to convert the mixed fractions to a improper fraction.

`21 (1)/(5) = (21*5 + 1 )/(5) = (105 + 1)/(5) = (106)/(5)`

`19 (1)/(4) = (19*4 + 1 )/(4) = (76 + 1)/(4) = (77)/(4)`

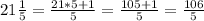
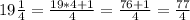
And substract:

`(106)/(5) - (77)/(4)`

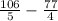
The common denominator for the function 5*4 = 20

`(106)/(5) - (77)/(4) = (106*4 - 77*5)/(20) = (428-385)/(20)= (39)/(20) = 1 (19)/(20)`

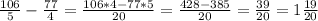
Matt shaved 1 19/20 mins.

Now you have to calculate substract 1 19/20 to 2 1/2 to know how many more minutes needs Matt lower his time race.

`2 (1)/(2) - (39)/(20) = (5)/(2) - (39)/(20) = (50)/(20)-(39)/(20) = (11)/(20)`