Answer:
A. $301
B. $721
Explanation:
Let $x be the amount of money they raised.
Rowena tried to put the $1 bills into two equal piles and found one left over at the end, then
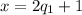
Polly tried to put the $1 bills into three equal piles and found one left over at the end, then
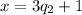
Frustrated, they tried 4, 5, and 6 equal piles and each time had $1 left over, then
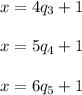
Finally Rowena put all the bills evenly into 7 equal piles, and none were left over, then

This means
 is divisible by 2, 3, 4, 5 and 6 without remainder, so
is divisible by 2, 3, 4, 5 and 6 without remainder, so
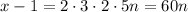
Hence,
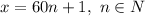
The smallest amount of money they could have raised is $301, because
 is divisible by 7.
is divisible by 7.
Now, the number
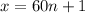 should be divisible by 7 and must be greater than 500.
should be divisible by 7 and must be greater than 500.
So,
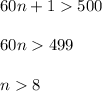
When n = 9,
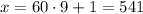 is not divisible by 7.
is not divisible by 7.
When n = 10,
 is not divisible by 7.
is not divisible by 7.
When n = 11,
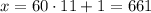 is not divisible by 7.
is not divisible by 7.
When n = 12,
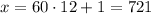 is divisible by 7.
is divisible by 7.
B. The least amount of money they could have raised is $721