Question

Prove that the triangle with vertices with (3,5), (-2,6), and (1,3) is a right triangle.

Answer 1

The triangle with vertices with (3, 5), (-2, 6), and (1, 3) is a right triangle.

Solution:

Given that the vertices of triangle are (3, 5), (-2, 6) and (1, 3)

Let us consider A(3, 5) B(-2, 6) C(1, 3)

If the sum of square of distance between two vertices is equal to the square of distance between third vertices, then the triangle is a right angled triangle.

By above definition, we get

`BC^(2) + CA^(2) = AB^(2)` ----- eqn 1

Where AB is the distance between vertices A and B

BC is the distance between vertices B and C

CA is the distance between vertices C and D

Distance between any two vertices of a triangle is given as

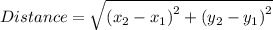`Distance =  \sqrt{\left(x_(2) -x_(1)\right )^(2) + \left(y_(2) -y_(1)\right)^(2)  }` ------- eqn 2

Step 1:

Let us find the distance between the vertices A(3,5) and B(-2,6)

By using equation 2, we get

`x_(1) = 3, x_(2) = -2, y_(1) = 5 \text { and } y_(2) = 6`

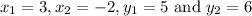
Distance between vertices A and B =
`\sqrt{(-2-3)^(2)+(6-5)^(2)}`

=
`\sqrt{(-5)^(2) + (1)^(2)}`

=
`\sqrt{(-5)^(2) + (1)^(2)}`

=
`√(25+1)`

=
`√(26) units`

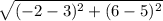
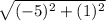
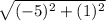
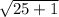
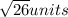
Step 2:

Let us find the distance between the vertices B(-2,6) and C(1,3)

By using equation 2, we get

`x_(1) = -2, x_(2) = 1, y_(1) = 6 \text { and } y_(2) = 3`

Distance between vertices B and C =
`\sqrt{(1-(-2))^(2)+(3-6)^(2)}`

=
`\sqrt{(1-(-2))^(2) + (3-6)^(2)}`

=
`\sqrt{3^(2)+9}`

=
`√(9+9)`

=
`√(18) \text { units }`

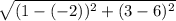
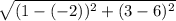
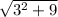
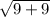
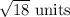
Step 3:

Let us find the distance between the vertices C(1,3) and D(3,5)

By using equation 2, we get

`x_(1) = 1, x_(2) = 3, y_(1) = 3 \text { and } y_(2) = 5`

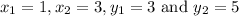
Distance between the vertices C and A

=
`\sqrt{(3-1)^(2) + (5-3)^(2)}`

=
`\sqrt{2^(2) + 2^(2)}`

=
`√(4+4)`

=
`√(8) units`

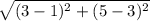
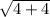
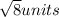
Step 4:

By using equation 1,

`BC^(2) + CA^(2) = AB^(2)`

`(√(18))^(2) + (√(8))^(2) = (√(26))^(2)`

18 + 8 = 26

26 = 26

Hence the condition is satisfied. So the given triangle with vertices with (3,5), (-2,6), and (1,3) is a right triangle.