Question

Please help!

Determine if the function shows a linear relationship or an absolute value relationship. Then evaluate the function for the indicated value of x.
a. f(x) = |x – 3| – 2; x = –5
b. g(x) = 1.5x; x = 0.2
c. p(x) = |7 – 2x|; x = –3

Answer 1

I think it’s b:g(x)=1.5x; x=0.2

Answer 2

(a) Absolute value relationship, f(-5)=6

(b) Linear relationship, g(0.2)=0.3

(c) Absolute value relationship, p(-3)=13

Explanation:

A modulas function always represents an absolute value relationship.

A polynomial function with degree 1 is always represents a linear function.

(a)

The given function is

`f(x)=|x-3|-2`

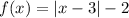
It is a modulas function, so it represents an absolute value relationship.

Substitute x=-5 in the given function.

`f(-5)=|-5-3|-2\Rightarrow 8-2=6`

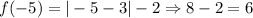
Therefore the value of function at x=-5 is 6.

(b)

The given function is

`g(x)=1.5x`

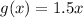
It is a linear function, so it represents a linear relationship.

Substitute x=0.2 in the given function.

`g(0.2)=1.5(0.2)=0.3`

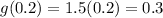
Therefore the value of function at x=0.2 is 0.3.

(c)

The given function is

`p(x)=|7-2x|`

It is a modulas function, so it represents an absolute value relationship.

Substitute x=-3 in the given function.

`p(-3)=|7-2(-3)|\Rightarrow |7+6|=13`

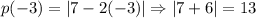
Therefore the value of function at x=-3 is 13.