Answer:
The current needed to transmit Power of 4 W is 28.47 A
Solution:
As per the question:
Length of the antenna,
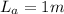
Frequency,
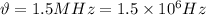
Power transmitted,
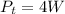
Now,
For a monopole antenna:
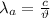
where
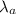 = wavelength transmitted by the antenna
= wavelength transmitted by the antenna
c = speed of light in vacuum
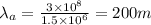
Now,
Since, the value of
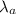 >>
>>
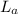 thus the monopole is a Hertian monopole.
thus the monopole is a Hertian monopole.
The resistance is calculated as:
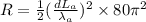
![R = (1)/(2)(\frac{1}{200)^(2)* 80\pi^(2) = 9.869* 10^(- 3) = 9.869 m\Omega]()
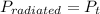
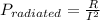
Now, the current I is given by:
