Answer:
The ball will take 4.05 seconds to hit the ground.
Explanation:
we have
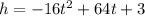
This is a quadratic equation (vertical parabola) open down
The vertex is a maximum
we know that
The ball hit the ground when h=0
Solve the quadratic equation
For h=0
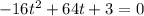
The formula to solve a quadratic equation of the form
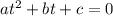 is equal to
is equal to
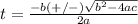
in this problem we have
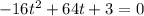
so
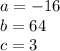
substitute in the formula
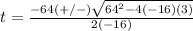
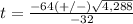
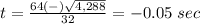 ---> the time cannot be a negative number
---> the time cannot be a negative number
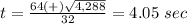
therefore
The ball will take 4.05 seconds to hit the ground.