Answer:
The factors of
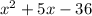 is (x+9) and (x-4)
is (x+9) and (x-4)
Solution:
From question, given that
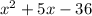
To factorise the above equation, follow the below steps:
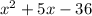
5x can be rewritten as 9x – 4x. hence the above equation becomes,
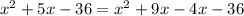
Take “x” as common from first two terms and “4” as common from next two terms. Thus the above equation becomes,
= x(x+9)-4(x+9)
Since x+9 is common in both the terms, the above equation becomes,
= (x+9) (x-4)
Thus factors of
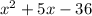 are (x+9) and (x-4)
are (x+9) and (x-4)