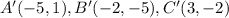Question

Which of the following are the vertices of the image of the figure below under the translation (x,y) (x+1,y-3) ? (-6,4)a (2, 1)c (- 3, - 2) b

Answer 1

C: (-5,1), (3,-2), (-2,-5)

Answer 2

The vertices of the image are
`A'(-5,1),B'(-2,-5),C'(3,-2)`

Explanation:

we know that

The rule of the translation is

`(x,y) -----> (x+1,y-3)`

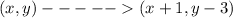
That means ----> The translation is one unit at right and three units down

we have

`A(-6,4), B(-3,-2),C(2,1)`

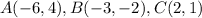
Applying the rule of translation

`A(-6,4) -----> A'(-6+1,4-3)\\A'(-5,1)`

`B(-3,-2) -----> B'(-3+1,-2-3)\\B'(-2,-5)`

`C(2,1) ----> C'(2+1,1-3)\\C'(3,-2)`

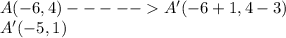
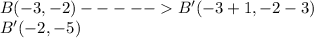
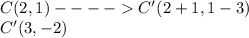
therefore

The vertices of the image are

`A'(-5,1),B'(-2,-5),C'(3,-2)`