Question

3. Write the quadratic function f (x) = x2 + 6x + 14 in vertex form.

Answer 1

well, let's start off by doing some grouping, what we'll be doing is so-called "completing the square" as in a perfect square trinomial, since that's what the vertex form of a quadratic uses.

`\bf f(x) = (x^2+6x)+14\implies f(x) = (x^2+6x+\boxed{?}^2)+14`

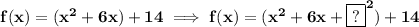
well, darn, we have a missing number for our perfect trinomial, however let's recall that in a perfect square trinomial the middle term is really the product of 2 times the term on the left and the term on the right without the exponent, so then we know that

`\bf 2(x)\boxed{?} = 6x\implies \boxed{?}=\cfrac{6x}{2x}\implies \boxed{?}=3`

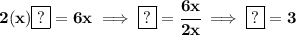
well then, that's our mystery guy, now, let's recall all we're doing is borrowing from our very good friend Mr Zero, 0, so if we add 3², we also have to subtract 3².

`\bf ~~~~~~\textit{vertical parabola vertex form} \\\\ y=a(x- h)^2+ k\qquad \begin{cases} \stackrel{vertex}{(h,k)}\\\\ \stackrel{`